Series temporales con ARIMA I
ARIMA
Muchos hemos estudiado en la carrera los modelos “clásicos” ARIMA sin enterarnos de nada. No echo la culpa a mis profes de estadística, son temas muy teóricos y con formulación matemática extensa que se dan con muy poca práctica, por lo que terminamos sin saber realmente ni cómo, ni donde aplicarlo.
Ahora que mi profe soy yo, me he decidido a entender estos modelos para ver si les saco partido para el pronóstico de series temporales. Me han sorprendido gratamente, son modelos robustos y poderosos, funcionan muy bien, y no resultan tan difíciles de aplicar como pensaba por lo que me vamos a dedicarles al menos 2 artículos, empecemos:
Los modelos ARIMA son acrónimo de su definición en inglés autoregressive (AR) integrated (I) moving average (MA) que traducido al panocho es algo así como modelo autorregresivo integrado de media móvil.
El modelo ARIMA genera una serie temporal a partir de 3 parámetros (p,d,q) llamados órdenes del modelo ARIMA(p,d,q). Como indica el acrónimo se trata de 3 modelos distintos unidos: AR + I + MA. Básicamente lo que dicen los libros es que los ARIMA son la forma generalizada de los modelos ARMA(p,q) que sirven para descomponer, analizar o pronosticar series temporales estacionarias.
SERIES ESTACIONARIAS
Los modelos ARIMA solo se pueden aplicar a series temporales que representan procesos estacionarios. Intuitivamente este concepto se refiere a que las propiedades (media y varianza) de la serie no varían con respecto al intervalo de tiempo que tomemos. Es decir, a series SIN TENDENCIA, SIN CICLOS, y con VARICIONES más o menos homogéneas.
Las series temporales estacionarias son habituales del mundo físico, pero no así en ciencias económicas o sociales donde suele haber tendencias y variaciones no homogéneas en el tiempo.
Si los modelos arima son ampliamente usados es porque, como veremos, se puede transformar cualquier serie no estacionaria y convertirla en estacionaria con transformaciones matemáticas “sencillas”.
ACF y PACF. Correlogramas
Para saber cómo aplicar los modelos ARIMA tendremos que aprender a interpretar las gráficas de autocorrelación ACF y autocorrelación parcial PACF de una serie temporal. Estas gráficas nos ayundan a estimar los órdenes (recuerda…los 3 parámetros) (p,d,q) del modelo ARIMA.
En \(R\) tenemos mil formas de usar ARIMA, pero las librerías astsa y forecast son las más completas y fáciles. La librería forecast es imprescindible para pronóstico de series temporales con muchos otros modelos programados.
Aunque existe de la función de RBase acf() para representar las gráficas de autocorrelación o correlogramas, prefiero pintarlas con cualquiera de estas otras funciones :
acf2()del paqueteastsao mejor con:ggtsdisplay()otsdisplay()del paqueteforecast..
Veamos un ejemplo:
# Gráficas ACF y PACF de la serie Nile con forecast
library(forecast)
ggtsdisplay(Nile,main='Caudal anual max del río Nilo')
# correlogramas con astsa de la misma serie diferenciada
library(astsa)
acf2(diff(Nile))
## [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10] [,11] [,12]
## ACF -0.4 -0.04 0.03 -0.09 0.00 0.05 -0.13 0.23 -0.08 -0.18 0.15 -0.04
## PACF -0.4 -0.25 -0.12 -0.17 -0.16 -0.07 -0.22 0.07 0.02 -0.23 -0.10 -0.10
## [,13] [,14] [,15] [,16] [,17] [,18] [,19] [,20]
## ACF 0.07 0.01 -0.08 0.09 -0.10 0.07 -0.01 0.00
## PACF 0.01 -0.02 -0.07 0.00 -0.13 0.09 -0.01 -0.02En cualquiera de estas representaciones, la banda entre las líneas azules intermitentes indican la zona de valores NO SIGNIFICATIVOS de correlación, que a efectos prácticos equivale a cero o NO correlación.
Por el contrario en la zona por encima o por debajo de dichas bandas, la correlación es significativa.
ARMA - Interpretación de ACF y PACF
La gráfica ACF pinta en cada rezago o lag, el valor de autocorrelación. Esto se hace calculando el coeficiente de correlación de dos vectores o columnas. En la columna 1 ponemos la serie \(X_t\) y en la dos la serie rezagada un intervalo \(X_{t-1}\).
Luego con de estas dos columnas se calcula el coeficiente de correlación entre ambas y pintamos ese valor en la gráfica, esto sería para x lag=1. Si corremos la columna 2 un retraso más y volvemos a calcular el coef.correlación entre \(X_t\) (col1) y \(X_{t-2}\) (hoy vs. anteayer). Esto lo podemos hacer n veces, hasta que llegamos al último intervalo de la serie temporal, aunque cada vuelta tenemos una fila menos y por tanto es menos representativa, por eso siempre interpretamos los primeros valores (lag), que son los importantes.
Los valores de ACF van de -1 a 1, Un valor próximo a 1 indica una gran correlación entre intervalos, si es próximo a -1 la correlación es inversa (los valores de hoy tienden a subir cuando los de ayer bajan), y uno próximo a 0 significa que las columnas comparadas son independientes = no podemos predecirlos (nada nos dice el valor de ayer respecto al que tenemos hoy).
La gráfica PACF es la derivada o pendiente de la ACF y nos indica la correlación parcial entre los intervalos, descontando el efecto del resto.
Resulta que estas gráficas nos pueden dar los órdenes para ajustar un modelo ARIMA, la clave está en interpretarlas según la siguiente tabla:
| AR(p) | MA(q) | ARMA(p,q) | |
|---|---|---|---|
| ACF | varios puntos con coef>0 decayendo | 0 excepto los q primeros |
varios puntos con coef>0 decayendo |
| PACF | 0 excepto los p primeros |
varios puntos con coef>0 | varios puntos con coef>0 |
Como regla, la PACF define el orden de AR(p) y la ACF el orden de MA(q). Otra cosa a tener encuentra para su interpretación es que hay que fijarse bien en los valores absolutos de los primeros datos, obviando las inversiones abajo-arriba que solo son indicadores de algún coeficiente negativo del modelo, pero no afectan al órden (p,q).
Veamos unos ejemplos de series ARMA generadas automáticamente y sus gráficas ACF/PACF, trata de ver las caracteristicas de la tabla para identificar los órdenes:
Una última anotación: hay que procurar siempre elegir el modelo más simple de los posibles, para ajustarse al principio de parsimonia o navaja de Ockham que dice que ante varios modelos con iguales resultados, la hipótesis que tiene menor número de supuestos suele ser la correcta.
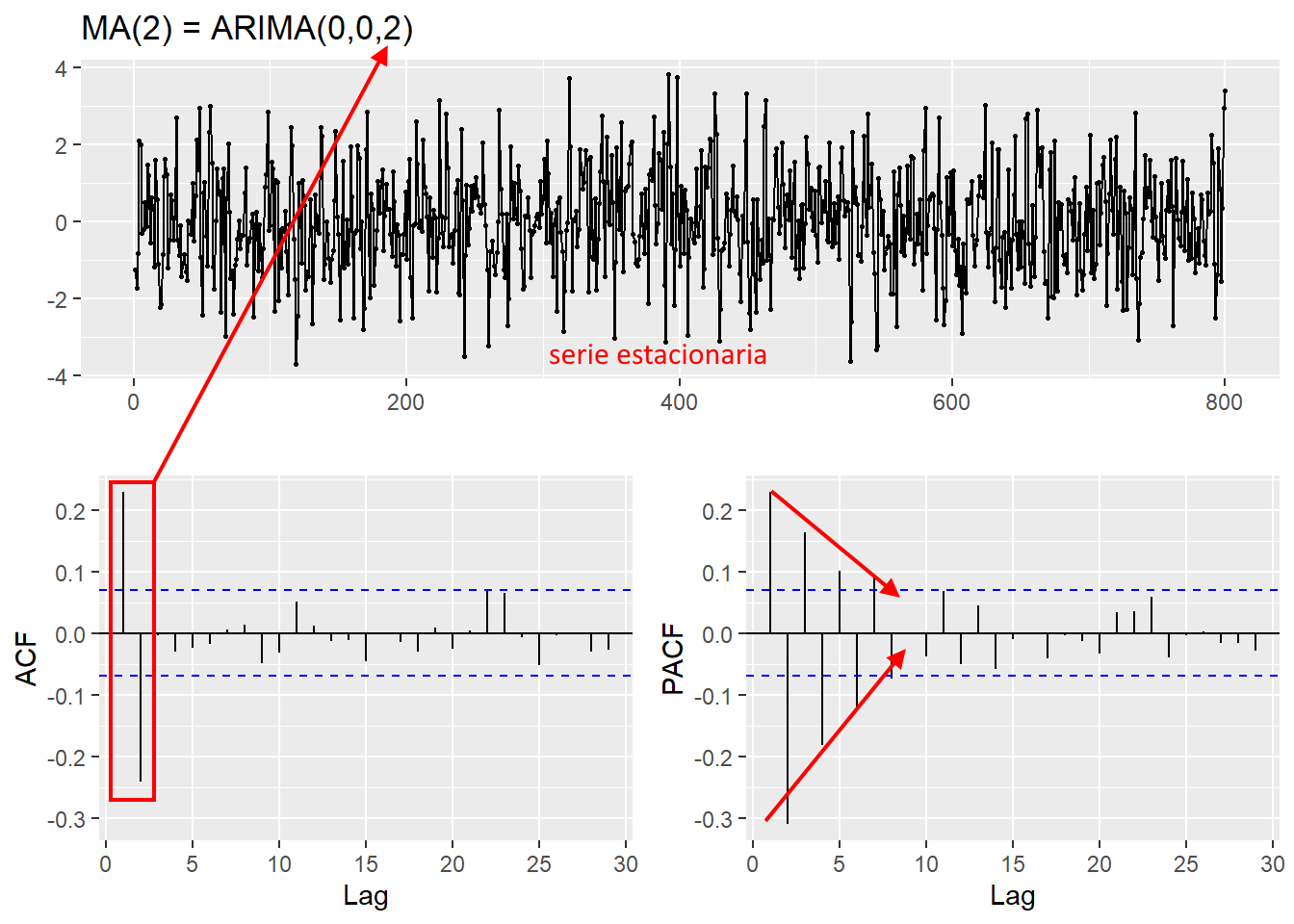
# Simulamos una serie arima(0,0,q)= MA(q)
# usamos la funion arima.sim de Rbase
MA <- arima.sim(model=list(order=c(0,0,2),ma= c(0.8,-0.5)), n=800)
# Visualizamos las autocorrelaciones
ggtsdisplay(MA, main="MA(2) = ARIMA(0,0,2)")
# Simulamos una serie arima(p,0,0)= AR(p)
AR <- arima.sim(model=list(order=c(1,0,0),ar= 0.7), n=600)
ggtsdisplay(AR,main="AR(1)=ARIMA(1,0,0)")
Si hay muchos valores de ACF altos(significativos), la serie es NO estacionaria y habrá que agregar una diferenciación con d como pasa en la gráfica de la serie de caudales máximos del Nilo.
Si los valores de ACF son todos nulos (entre las bandas azules) se trata de ruido blanco ARIMA(0, 0, 0). Si la diff(1) es ruido blanco es un paseo aleatorio o randon walk ARIMA(0, 1, 0) o I(1) es equivalente a \(X_t = X_{t − 1} + ε_t\).
Otro caso especial es cuando se dan ciertos valores altos en la ACF en ciclos, por ejemplo un pico en el lag 12, 24, 36. En estos casos hay ciclos estacionales o anual ( ¡Ojo! no confundir con lo que vimos antes que es estacionariedad). El modelo completo arima los tiene en cuenta añadiendo complejidad con el ciclo estacional que se define con 3 parámetros adicionales ARIMA(p,d,q)(P,D,Q)m.
I -Integracion o transformacion de series
Como la matemática de estos modelos ARMA() está mas que probada, es “sencilla” y funciona bien, se buscó la forma de aplicarlos a series que no cumplen la condición de estacionariedad, es decir aquellas con tendencia, ciclos o varianza no homogenea.
La manera más simple de transformar la serie a estacionaria es diferenciándola. Esto lo haremos para quitar las tendencias y que consiste simplemente en restar al valor de hoy, el de ayer, y así quedarnos con una serie temporal nueva llamada de diferencias, en \(R\) se hace con la función diff(x).
La I de AR-I-MA indica el orden de integración o diferenciación (número de veces que hay que diferenciar recursivamente) la serie origen para convertirla en estacionaria. Esto permite ampliar el rango de uso a series no estacionarias en media, es decir a las que tienen tendencias.
Diferenciar una serie es calcular la nueva serie \(Y_t\) tal que : \(Y_t=X_t-X_{t−1}\).
Según la nomeclatura de los modelos ARIMA(p,d,q), el número de integraciones o diferenciaciones que hay que hacer a una serie para convertirla en estacionaria se da con el parámetro d que toma valores entre 0 y 1 habitualmente.
En \(R\) lo tenemos fácil, pues el paquete forecast cuenta con dos funciones ndiffs y nsdiffs(), que nos dicen el número de diferenciaciones que hay que hacer a la serie, es decir, el orden d, y el D estacional en caso de que muestren alguno.
RESUMEN DEL PROCESO DE AJUSTE
Antes de ver casos prácticos en el siguiente artículo, vamos a resumir un procedimiento de trabajo que nos guíe para realizar un ajuste ARIMA a una serie temporal cualquiera.
Siguiendo los pasos conseguiremos obtener los órdenes del modelo ARIMA(p,d,q)(P,D,Q)s y realizar pronósticos. Como verás hay cosas que no he comentado en este artículo, pues se haría muy largo, pero que trataremos en los casos prácticos.
El proceso que sigo es:
- Pintar la serie temporal (\(X_t\)) e identificar valores, NA o inusuales (outliers). En tal caso uso
forecast::tsclean(x). - Analizar si los datos parecen o no ESTACIONARIOS mirando la gráficas ACF/PACF. Alternativamente o después de analizar el gráfico, podemos usar las funciones
ndiffs(), para obtener el ordendde diferenciación y pintar las nuevas gráficas ACF/PACF de la serie \(diff(X_t)\). También podemos usar test como:adf.test(x, alternative = "stationary")para saber si es o no estacionaria. - Comprobar si tiene ciclos estacionales (de lag=S) con
nsdiffs(), en tal caso pintar ACF y PACF dediff(xlag=S)e iniciar el proceso desde el paso 1 para el ciclo. - Si en la gráfica apreciamos que la varianza no es homogénea, hay que usar algún método de transformación de varianza como tomar
log(x)oBox-Cox(x)calculandolambda. - Examinar las ACF/PACF y proponer modelos
ARIMA(p,d,q)con la interpretación y guía dada en la tabla 1. Alternativamente usarauto.arima()para hallar el mejor modelo de ajuste automático (que no siempre es mejor). - Ver los resultados de AICc,AIC o BIC de los modelos
astsa::sarima(x,p,d,q)para elegir el mejor (el que tenga menor BIC, AIC.. es el mejor), también conaccuracy(x). - Chequear los gráficos de residuos del modelo, por ejemplo con la función
sarima()ocheckresiduals()para comprobar que sea ruido blanco, pues en caso contrario todavía hay información relevante en ellos y el modelo no es completo —> añadir algún orden. - Hacer pronóstico con
sarima.for(x, n.ahead = 20, p = 1, d = 1, q = 1)o conforecast(fit,h = n_test).
Parece complejo, pero luego no lo es tanto, y los resultados de los pronósticos son bastante buenos. En el siguiente post veremos algunos casos prácticos y verás todo más claro.
En resumen hacemos esto:

